Question

The polynomial of degree 4, P(x) has a root of multiplicity 2 at x = 4 and roots of multiplicity 1 at x = 0 and x = - 3 3. It goes through the point (5, 28) . Find a formula for P(x)

Answer 1

The complete polynomial will be:

`P(x)=(7)/(10)x(x+3)(x-4)^2`

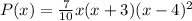
Explanation:

If one root has multiplicity 2 at x = 4, the factor can write as:

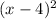`(x-4)^(2)` (1)

Now, another root has a multiplicity 1 at x=0 and x=-3, then the factors will be:

`x` (2)

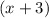`(x+3)` (3)

Putting (1),(2), and (3) together we can construct the polynomial.

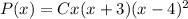`P(x)=Cx(x+3)(x-4)^2` (4)

C is a constant value

We need to use the point (5, 28) to find the constant C. 5 is the x value and 28 is the P(x) value. Replacing these values into the (4) equation:

`28=C5(5+3)(5-4)^2`

`28=C5(8)(1)^2`

`28=40C`

`C=(28)/(40)`

`C=(7)/(10)`

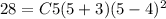
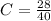
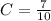
Finally, the complete polynomial will be:

`P(x)=(7)/(10)x(x+3)(x-4)^4`

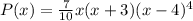
I hope it helps you!