Answer:
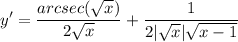
General Formulas and Concepts:
Algebra I
- Exponential Rule [Rewrite]:
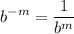
- Exponential Rule [Root Rewrite]:
![\displaystyle \sqrt[n]{x} = x^{(1)/(n)}](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/pi5gzwebrzl682dhc5849e.png)
Calculus
Derivatives
Derivative Notation
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Derivative Rule [Product Rule]:
![\displaystyle (d)/(dx) [f(x)g(x)]=f'(x)g(x) + g'(x)f(x)](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/s9b4uuk11h1mreum0i8io5.png)
Derivative Rule [Chain Rule]:
![\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/4e7e93dqa2auubmnlpfb3w.png)
Arctrig Derivative:
![\displaystyle (d)/(dx)[arcsec(u)] = (u')/(|u|√(u^2 - 1))](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/uvtvvhpi004uau88ryevu7.png)
Explanation:
Step 1: Define
Identify
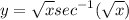
Step 2: Differentiate
- Rewrite:
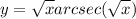
- Product Rule:
![\displaystyle y' = (d)/(dx)[√(x)]arcsec(√(x)) + √(x)(d)/(dx)[arcsec(√(x))]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/uapkppruy0orch79d8g87b.png)
- Chain Rule:
![\displaystyle y' = (d)/(dx)[√(x)]arcsec(√(x)) + \bigg[ √(x)(d)/(dx)[arcsec(√(x))] \cdot (d)/(dx)[√(x)] \bigg]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/93tbs2vslxxdaq22r4y3ce.png)
- Rewrite [Exponential Rule - Root Rewrite]:
![\displaystyle y' = (d)/(dx)[x^\bigg{(1)/(2)}]arcsec(√(x)) + \bigg[ √(x)(d)/(dx)[arcsec(√(x))] \cdot (d)/(dx)[x^\bigg{(1)/(2)}] \bigg]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/d99m2nq582deo967h8zccm.png)
- Basic Power Rule:
![\displaystyle y' = (1)/(2)x^\bigg{(1)/(2) - 1}arcsec(√(x)) + \bigg[ √(x)(d)/(dx)[arcsec(√(x))] \cdot (1)/(2)x^\bigg{(1)/(2) - 1} \bigg]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/horapjssxuw9bn0ussn8u5.png)
- Simplify:
![\displaystyle y' = (1)/(2)x^\bigg{(-1)/(2)}arcsec(√(x)) + \bigg[ √(x)(d)/(dx)[arcsec(√(x))] \cdot (1)/(2)x^\bigg{(-1)/(2)} \bigg]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/ajc1yeeoqgd3bwtp2ldehp.png)
- Rewrite [Exponential Rule - Rewrite]:
![\displaystyle y' = \frac{1}{2x^\bigg{(1)/(2)}}arcsec(√(x)) + \bigg[ √(x)(d)/(dx)[arcsec(√(x))] \cdot \frac{1}{2x^\bigg{(1)/(2)}} \bigg]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/axxmw4jojscocqam3atrxf.png)
- Rewrite [Exponential Rule - Root Rewrite]:
![\displaystyle y' = (1)/(2√(x))arcsec(√(x)) + \bigg[ √(x)(d)/(dx)[arcsec(√(x))] \cdot (1)/(2√(x)) \bigg]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/xi4nun7p2h72z0bmtdyfzw.png)
- Arctrig Derivative:
![\displaystyle y' = (1)/(2√(x))arcsec(√(x)) + \bigg[ √(x)\frac{1}{|√(x)|\sqrt{(√(x))^2 - 1}} \cdot (1)/(2√(x)) \bigg]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/kustelbq7zpu5xxw8lr19m.png)
- Simplify:
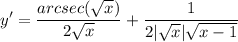
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Derivatives
Book: College Calculus 10e