Question

Imagine that you need to compute e^0.4 but you have no calculator or other aid to enable you to compute it exactly, only paper and pencil. You decide to use a third-degree Taylor polynomial expanded around x = 0. Use the fact that e^0.4 < e < 3 and the Error Bound for Taylor Polynomials to find an upper bound for the error in your approximation.

I error l ≤

Answer 1

upper bound for the error, | Error | ≤ 0.0032

Explanation:

Given the data in the question;

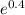`e^{0.4` < e < 3

Using Taylor's Error bound formula

| Error | ≤ ( m / ( N + 1 )! )
`| x-a |^{N+1`

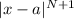
where m =
`| f^(N+1 )(x) |`

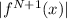
so we have

| Error | ≤ ( 3 / ( 3 + 1 )! )
`|` -0.4
`|`⁴

| Error | ≤ ( 3 / 4! )
`|` -0.4
`|`⁴

| Error | ≤ ( 3 / 24 )
`|` -0.4
`|`⁴

| Error | ≤ ( 0.125 )
`|` -0.0256
`|`

| Error | ≤ ( 0.125 ) 0.0256

| Error | ≤ 0.0032

Therefore, upper bound for the error, | Error | ≤ 0.0032