Question

Thirsty Cactus Corp. just paid a dividend of $1.50 per share. The dividends are expected to grow at 25 percent for the next 9 years and then level off to a 5 percent growth rate indefinitely. If the required return is 13 percent, what is the price of the stock today?

Answer 1

$143.40

Step-by-step explanation:

The dividend for the next year =
`\text{ current year dividend} * (1 + \text{growth})`

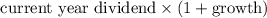
= $ 1.50 x (1 + 0.13)

= 1.50 x 1.30

= $ 1.95

The dividend in the second year = 1.95 x 1.30

= $ 2.54

Similarly, the dividend for the year 9 is =
`$1.50 * (1.30)^9$`

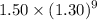
= $ 15.91

The value of the stock at the end of year 9,

`$=\frac{\text{Dividend of year 10}}{\text{(Required rate of return - Growth rate)}}$`

`$=(15.91*1.05)/(0.13-0.05)$`

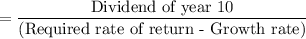
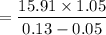
= $ 208.81

The present value factor
`$=(1)/((1+r)^n)$`

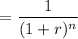
where, r = rate of interest = 13% = 0.13

n = years (1 to 9)

So, the present value factor for the 2nd year is
`$=(1)/((1+0.13)^2)$`

`$=(1)/((1.13)^2)$`

`$=(1)/(1.2769)$`

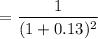
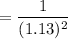
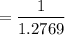
= 0.783147

Therefore, the price of the stock today is calculated as to be $ 143.40