Answer:
$143.40
Step-by-step explanation:
The dividend for the next year =
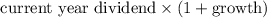
= $ 1.50 x (1 + 0.13)
= 1.50 x 1.30
= $ 1.95
The dividend in the second year = 1.95 x 1.30
= $ 2.54
Similarly, the dividend for the year 9 is =

= $ 15.91
The value of the stock at the end of year 9,
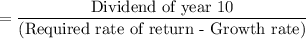
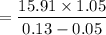
= $ 208.81
The present value factor
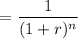
where, r = rate of interest = 13% = 0.13
n = years (1 to 9)
So, the present value factor for the 2nd year is

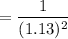
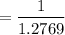
= 0.783147
Therefore, the price of the stock today is calculated as to be $ 143.40