Question

Cough-a-Lot children’s cough syrup is supposed to contain 6 ounces of medicine per bottle. However, since the filling machine is not always precise, there can be variation from bottle to bottle. The amounts in the bottles are normally distributed with σ = 0.3 ounces. A quality assurance inspector measures 10 bottles and finds the following (in ounces): 5.95 6.10 5.98 6.01 6.25 5.85 5.91 6.05 5.88 5.91 Are the results enough evidence to conclude that the bottles are not filled adequately at the labeled amount of 6 ounces per bottle? State the hypothesis you will test. Calculate the test statistic. Find the P-value. What is the conclusion?

Answer 1

Following are the solution to the given question:

Explanation:

Performance of the student's t-test as
`n=10`

n<30

Calculating the Null hypothesis:

`\to H_0 : \mu =6`

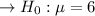
Calculating the Alternative Hypothesis:

`\to H_1 : \mu \\eq 6`

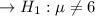
Calculating the level of significance
`=0.05`

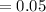
Calculating the test statistic:

`\to \bar{x}=(5.95 +6.10+ 5.98+ 6.01 +6.25+ 5.85 +5.91+ 6.05 +5.88+ 5.91)/(10)\\\\=(59.89)/(10)\\\\=5.989`

Because of the population standard deviation, perform z test

`z=\frac{\bar{x}-\mu}{(\sigma)/(√(n))}`

`=(5.989-6)/((0.3)/(√(10) )) \\\\=-0.116`

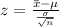
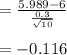
Decision:

Comparison of p-value test statistics and decision-making.

Hypothesis P<0.05 Reject.

P>0.05 No hypothesis rejecting zero.

P-Value = 0.907653.

At p<0.05 the result is not significant.

Null hypothesis not to be rejected.

Accepting the null hypothesis.

Conclusion:

Its assertion that the containers were not refilled appropriately by the specified amount of 6 ounces/bottle doesn't contain substantial proof. Bottles with mean = 6 ounces are suitably filled.