Answer:
The parabola has the following characteristics:
(i)

(ii)
![Ran\{f(x)\} = (-\infty, 1]](https://img.qammunity.org/2022/formulas/mathematics/high-school/8yf3ch4jgpyy0e41ucph02l4hk6682pa95.png)
(iii) The parabola has an absolute maximum since
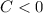 .
.
(iv) The vertex parameter of the parabola is -2.
Explanation:
Let suppose that parabola has a vertical axis of symmetry. From Analytical Geometry, the vertex form of the equation of the parabola is defined by the following formula:
 (1)
(1)
Where:
 - Independent variable.
- Independent variable.
 - Dependent variable.
- Dependent variable.
 ,
,
 - Coordinates of the vertex.
- Coordinates of the vertex.
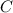 - Vertex parameter.
- Vertex parameter.
If we know that
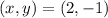 and
and
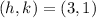 , then the vertex parameter of the parabola is:
, then the vertex parameter of the parabola is:
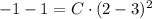
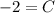
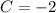
According to this information, we find the following characteristics:
(i)

(ii)
![Ran\{f(x)\} = (-\infty, 1]](https://img.qammunity.org/2022/formulas/mathematics/high-school/8yf3ch4jgpyy0e41ucph02l4hk6682pa95.png)
(iii) The parabola has an absolute maximum since
 .
.
(iv) The vertex parameter of the parabola is -2.