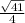Question

Let (-5. 4) be a point on the terminal side of ø
Find the exact values of cos, csc , and tan

Answer 1

`\cos(x) = - (5)/( √(41) )`

`\csc(x) = ( √(41) )/(4)`

`\tan(x) = - (4)/(5)`

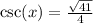
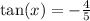
Explanation:

We know that (-5,4) is the terminal side. This means out legs will measure 5 and 4 if we graph it on a triangle.

We need to find the cos, csc, and tan measure of this point.

We can find cos by using the formula of

`\cos(x) = (adj)/(hyp)`

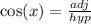
The adjacent side is -5 and we can find the hypotenuse by doing pythagorean theorem.

`{ - 5}^(2) + {4}^(2) = √(41)`

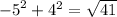
So using the info the answer is

`\cos(x) = ( - 5)/( √(41) )`

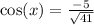
We can find tan but first me must find sin x.

`\sin(x) = (opp)/(hyp)`

`\sin(x) = (4)/( √(41) )`

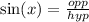
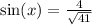
So now we just use this identity,

`\tan(x) = \sin(x) / \cos(x)`

`\tan(x) = ( (4)/( √(41) ) )/( ( - 5)/( √(41) ) ) = - (4)/(5)`

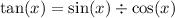
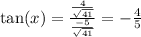
So tan x=

`- ( 4)/(5)`

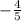
We can find csc by taking the reciprocal of sin so the answer is easy which is

`( √(41) )/(4)`