Question

In what ratio of line x-y-2=0 divides the line segment joining (3,-1) and (8,9)?​

Answer 1

• Let the given points ( 3 , -1 ) and ( 8 , 9 ) be A and B respectively. Let A ( 3 , - 1 ) be ( x₁ , y₁ ) and B ( 8 , 9 ) be ( x₂ , y₂ ). Let the point P ( x , y ) divides the line segment of joining points A ( 3 , -1 ) and ( 8 , 9 ) in the ratio m : n. Let m be m₁ and n be m₂ We know that :

`\large{ \tt{❁ \: USING \: INTERNAL \: SECTION \: FORMULA: }}`

`\large{ \bf{✾ \: P(x \:, y \: ) = ( (m_(1)x_(2) + m_(2)x_(1))/(m_(1) + m_(2)) \: ,\: (m_(1)y_(2) + m_(2)y_(1))/(m_(1) + m_(2))) }}`

`\large{ \bf{⟹ \: ( (8m + 3n)/(m + n) , \: (9m -n)/(m + n)) }}`

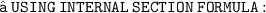
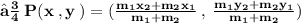
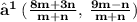
• Since point P lies on the line x - y - 2 = 0 ,

`\large{ \bf{ ⟼(8m + 3n)/(m + n) - (9m - n)/(m + n) - 2 = 0 }}`

`\large{ \bf{⟼ \: (8m + 3n - 9m + n)/(m + n) - 2 = 0 }}`

`\large{ \bf{⟼ \: (4n - m)/( m + n) - 2 = 0 }}`

`\large{⟼ \: \bf{ (4n - m)/(m + n )} = 2}`

`\large{ \bf{⟼ \: 4n - m = 2m + 2n}}`

`\large{ \bf{⟼ \: 4n -2 n = 2m + m}}`

`\large{ \bf{⟼2n = 3m}}`

`\large{ \bf{⟼ \: 3m = 2n}}`

`\large{ \bf{⟼ \: (m)/(n) = (2)/(3) }}`

`\boxed{ \large{ \bf{⟼ \: m : \: n = 2: \: }3}}`

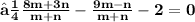
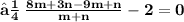
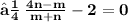
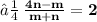
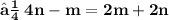
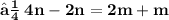
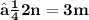
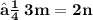
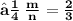
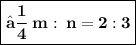
• Hence , The required ratio is 2 : 3 .

-Hope I helped! Let me know if you have any questions regarding my answer and also notify me , if you need any other help! :)

▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁