- Let the given points ( 3 , -1 ) and ( 8 , 9 ) be A and B respectively. Let A ( 3 , - 1 ) be ( x₁ , y₁ ) and B ( 8 , 9 ) be ( x₂ , y₂ ). Let the point P ( x , y ) divides the line segment of joining points A ( 3 , -1 ) and ( 8 , 9 ) in the ratio m : n. Let m be m₁ and n be m₂ We know that :
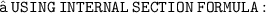
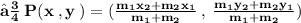
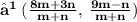
- Since point P lies on the line x - y - 2 = 0 ,
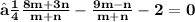

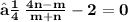
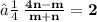
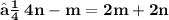
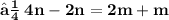
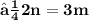

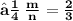

- Hence , The required ratio is 2 : 3 .
-Hope I helped! Let me know if you have any questions regarding my answer and also notify me , if you need any other help! :)
▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁