Question

A ball is thrown vertically upward with an initial velocity of 19 m/s. Its height, h(t)metres after t seconds, is given by the equation h(t) = -3t2 + 20t + 2.0.

The time taken by the ball to reach the maximum height is ________ seconds. Round your answer to the nearest tenth.

Answer 1

Explanation:

There are 2 different ways to do this: calculus and by completing the square. In this particular instance, calculus is WAY easier, and since I don't know for what class you are doing this, I'll do both ways. First the calculus way. We know the position equation, and the first derivative of the position is velocity. We also know that when the velocity is equal to 0 is when the object is at its max height. So we'll find the derivative first, then solve it for t:

If
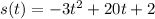`s(t)=-3t^2+20t+2` then the first derivative is

v(t) = -6t + 20 Solving for t requires that we set the velocity equal to 0 (again, this is where the object is at its max height), so

0 = -6t + 20 and

-20 = -6t so

t = 3.3 seconds. Now that we know that at 3.3 seconds the object is at its highest point, we sub that time into the position function to see where it is at that time:

s(3.3) =
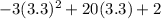`-3(3.3)^2+20(3.3)+2` and

s(3.3) = 35.3 meters.

Now onto the more difficult way...completing the square. Begin by setting the position function equal to 0 and then move over the constant to get:

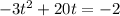`-3t^2+20t=-2` Since the leading coefficient is not a 1 (it's a 3), we have to factor out the 3, leaving us with:

`-3(t^2-(20)/(3)t)=-2` Now the rule is to take half the linear term, square it, and add it to both sides. Our linear term is
`(20)/(3)` and half of that is
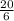`(20)/(6)`. Squaring that:

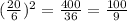`((20)/(6))^2=(400)/(36)=(100)/(9)`. We will add that in to both sides. On the left it's easy, but on the right we have to take into account that we still have that -3 sitting out front, refusing to be ignored. So we have to multiply it in when we add it to the right. Doing that gives us:

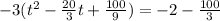`-3(t^2-(20)/(3)t+(100)/(9))=-2-(100)/(3)` We will clean this up a bit now. The reason we do this is because on the left we have created a perfect square binomial which will give us the time we are looking for to answer this question. Simplifying the right and at the same time writing the perfect square binomial gives us:

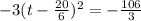`-3(t-(20)/(6))^2=-(106)/(3)` Now the last step is to move the constant back over and set the quadratic back equal to y:

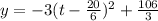`y=-3(t-(20)/(6))^2+(106)/(3)`. The vertex of this quadratic is

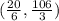`((20)/(6),(106)/(3))` where

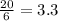`(20)/(6)=3.3` as the time it takes for the ball to reach its max height of

`(106)/(3)=35.3` meters.

I'd say if you plan on taking calculus cuz you're not there yet, you'll see that many of these types of problems become much simpler when you know it!