Question

Joe bikes at the speed of 30 km/h from his home toward his work. If Joe's wife leaves home 5 mins later by car, how fast should she drive in order to overtake him in 10 minutes.

Answer 1

Joe's wife must drive at a rate of 45km/hour.

Explanation:

We are given that Joe leaves home and bikes at a speed of 30km/hour. Joe's wife leaves home five minutes later by car, and we want to determine her speed in order for her to catch up to Joe in 10 minutes.

Since Joe bikes at a speed of 30km/hour, he bikes at the equivalent rate of 0.5km/min.

Then after five minutes, when his wife leaves, Joe is 5(0.5) or 2.5 km from the house. He will still be traveling at a rate of 0.5km/min, so his distance from the house can be given by:

`2.5+0.5t`

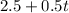
Where t represents the time in minutes after his wife left the house.

And since we want to catch up in 10 minutes, Joe's distance from the house 10 minutes after his wife left will be:

`2.5+0.5(10)=7.5\text{ km}`

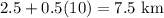
Let s represent the wife's speed in km/min. So, her speed times 10 minutes must total 7.5 km:

`10s=7.5`

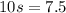
Solve for s:

`\displaystye s=0.75\text{ km/min}`

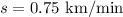
Thus, Joe's wife must drive at a rate of 0.75km/min, or 45km/hour.