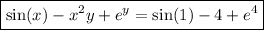Question

Answer pllllllleeeaaaaasssss

Answer 1

(3.1) … … …

`(\mathrm dy)/(\mathrm dx) = (2x-y)/(x-2y)`

Multiply the right side by x/x :

`(\mathrm dy)/(\mathrm dx) = \frac{2-\frac yx}{1-\frac{2y}x}`

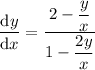
Substitute y(x) = x v(x), so that dy/dx = x dv/dx + v :

`x(\mathrm dv)/(\mathrm dx) + v = (2-v)/(1-2v)`

This DE is now separable. With some simplification, you get

`x(\mathrm dv)/(\mathrm dx) = (2-2v+2v^2)/(1-2v)`

`(1-2v)/(2-2v+2v^2)\,\mathrm dv = \frac{\mathrm dx}x`

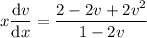
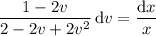
Now you're ready to integrate both sides (on the left, the denominator makes for a smooth substitution), which gives

`-\frac12\ln\left|2v^2-2v+2\right| = \ln|x| + C`

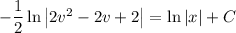
Solve for v, then for y (or leave the solution in implicit form):

`\ln\left|2v^2-2v+2\right| = -2\ln|x| + C`

`\ln(2) + \ln\left|v^2-v+1\right| = \ln\left(\frac1{x^2}\right) + C`

`\ln\left|v^2-v+1\right| = \ln\left(\frac1{x^2}\right) + C`

`v^2-v+1 = e^(\ln\left(1/x^2\right)+C)`

`v^2-v+1 = \frac C{x^2}`

`\boxed{\left(\frac yx\right)^2 - \frac yx+1 = \frac C{x^2}}`

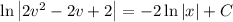
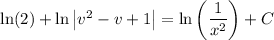
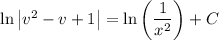
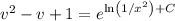
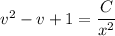
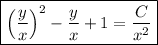
(3.2) … … …

`y' + \frac yx = (y^(-3/4))/(x^4)`

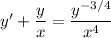
It may help to recognize this as a Bernoulli equation. Multiply both sides by
`y^(\frac34)` :

`y^(3/4)y' + \frac{y^(7/4)}x = \frac1{x^4}`

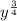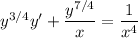
Substitute
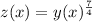`z(x)=y(x)^(\frac74)`, so that
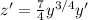`z' = \frac74 y^(3/4)y'`. Then you get a linear equation in z, which I write here in standard form:

`\frac47 z' + \frac zx = \frac1{x^4} \implies z' + \frac7{4x}z=\frac7{4x^4}`

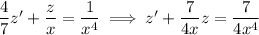
Multiply both sides by an integrating factor,
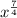`x^(\frac74)`, which gives

`x^(7/4)z'+\frac74 x^(3/4)z = \frac74 x^(-9/4)`

and lets us condense the left side into the derivative of a product,

`\left(x^(7/4)z\right)' = \frac74 x^(-9/4)`

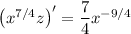
Integrate both sides:

`x^(7/4)z=\frac74\left(-\frac45\right) x^(-5/4)+C`

`z=-\frac75 x^(-3) + Cx^(-7/4)`

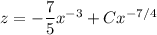
Solve in terms of y :

`y^(4/7)=-\frac7{5x^3} + \frac C{x^(7/4)}`

`\boxed{y=\left(\frac C{x^(7/4)} - \frac7{5x^3}\right)^(7/4)}`

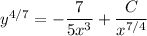
(3.3) … … …

`(\cos(x) - 2xy)\,\mathrm dx + \left(e^y-x^2\right)\,\mathrm dy = 0`

This DE is exact, since

`(\partial(-2xy))/(\partial y) = -2x`

`(\partial\left(e^y-x^2\right))/(\partial x) = -2x`

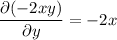
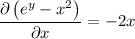
are the same. Then the general solution is a function f(x, y) = C, such that

`(\partial f)/(\partial x)=\cos(x)-2xy`

`(\partial f)/(\partial y) = e^y-x^2`

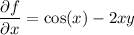
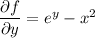
Integrating both sides of the first equation with respect to x gives

`f(x,y) = \sin(x) - x^2y + g(y)`

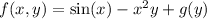
Differentiating this result with respect to y then gives

`-x^2 + (\mathrm dg)/(\mathrm dy) = e^y - x^2`

`\implies(\mathrm dg)/(\mathrm dy) = e^y \implies g(y) = e^y + C`

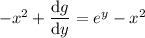
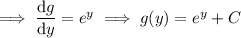
Then the general solution is

`\sin(x) - x^2y + e^y = C`

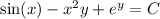
Given that y (1) = 4, we find

`C = \sin(1) - 4 + e^4`

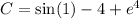
so that the particular solution is

`\boxed{\sin(x) - x^2y + e^y = \sin(1) - 4 + e^4}`