Question

PLZ help asap :-/
............................ ​

Answer 1

Step-by-step explanation:

[16]

`\underline{\boxed{\large{\bf{Option \; A!! }}}}`

Here,

• 
  `\rm { R_1}` = 2Ω
• 
  `\rm { R_2}` = 2Ω
• 
  `\rm { R_3}` = 2Ω
• 
  `\rm { R_4}` = 2Ω

We have to find the equivalent resistance of the circuit.

Here,
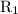`\rm { R_1}` and
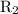`\rm { R_2}` are connected in series, so their combined resistance will be given by,

`\longrightarrow \rm { R_((1,2)) = R_1 + R_2} \\`

`\longrightarrow \rm { R_((1,2)) = (2 + 2) \; Omega} \\`

`\longrightarrow \rm { R_((1,2)) = 4 \; Omega} \\`

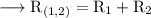
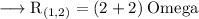
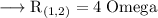
Now, the combined resistance of
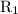`\rm { R_1}` and
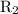`\rm { R_2}` is connected in parallel combination with
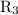`\rm { R_3}`, so their combined resistance will be given by,

`\longrightarrow \rm {(1)/( R_((1,2,3))) = (1)/(R_((1,2))) + (1)/(R_3) } \\`

`\longrightarrow \rm {(1)/( R_((1,2,3))) = \Bigg ( (1)/(4) + (1)/(2) \Bigg ) \;\Omega} \\`

`\longrightarrow \rm {(1)/( R_((1,2,3))) = \Bigg ( (1 + 2)/(4) \Bigg ) \;\Omega} \\`

`\longrightarrow \rm {(1)/( R_((1,2,3))) = \Bigg ( (3)/(4) \Bigg ) \;\Omega} \\`

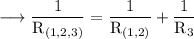
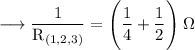
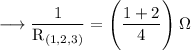
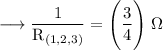
Reciprocating both sides,

`\longrightarrow \rm {R_((1,2,3))= (4)/(3) \;\Omega} \\`

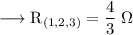
Now, the combined resistance of
`\rm { R_1}`,
`\rm { R_2}` and
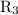`\rm { R_3}` is connected in series combination with
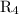`\rm { R_4}`. So, equivalent resistance will be given by,

`\longrightarrow \rm {R_((1,2,3,4))= R_((1,2,3)) + R_4} \\`

`\longrightarrow \rm {R_((1,2,3,4))= \Bigg ( (4)/(3) + 2 \Bigg ) \; \Omega} \\`

`\longrightarrow \rm {R_((1,2,3,4))= \Bigg ( (4 + 6)/(3) \Bigg ) \; \Omega} \\`

`\longrightarrow \rm {R_((1,2,3,4))= \Bigg ( (10)/(3) \Bigg ) \; \Omega} \\`

`\longrightarrow \bf {R_((1,2,3,4))= 3.33 \; \Omega} \\`

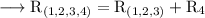
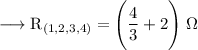
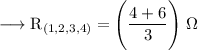
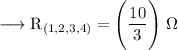
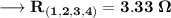
Henceforth, Option A is correct.

_________________________________

[17]

`\underline{\boxed{\large{\bf{Option \; B!! }}}}`

Here, we have to find the amount of flow of current in the circuit. By using ohm's law,

`\longrightarrow` V = IR

`\longrightarrow` 3 = I × 3.33

`\longrightarrow` 3 ÷ 3.33 = I

`\longrightarrow` 0.90 Ampere = I

Henceforth, Option B is correct.

____________________________

`\tt \purple{Hope \; it \; helps \; you, Army! \heartsuit } \\`