Answer:
726.34 cm/min
Explanation:
Volume of a sphere:
The volume of a sphere is given by the following equation:

In which r is the radius.
Implicit derivatives:
This question is solving by implicit derivatives. We derivate V and r, implicitly as function of t. So
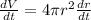
A spherical snowball is melting in such a way that its radius is decreasing at a rate of 0.2 cm/min.
This means that
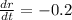
At what rate is the volume of the snowball decreasing when the radius is 17 cm.
This is
 when
when
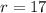
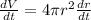
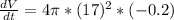

This means that the volume of the snowball is decreasing at a rate of 726.34 cm/min when the radius is 17 cm.