Answer:
(i) The value of m when t = 30 is 13.2
(ii) The value of t when the mass is half of its value at t=0 is 34.7
(iii) The rate of the mass when t=50 is -0.18
Explanation:
(i) The m value when t = 30 is:
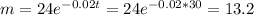
Then, the value of m when t = 30 is 13.2
(ii) The value of the mass when t=0 is:
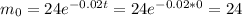
Now, the value of t is:
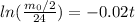
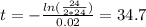
Hence, the value of t when the mass is half of its value at t=0 is 34.7
(iii) Finally, the rate at which the mass is decreasing when t=50 is:
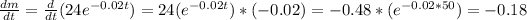
Therefore, the rate of the mass when t=50 is -0.18.
I hope it helps you!