Answer:
The height of the triangle is 8 centimeters.
The area of the rectangle is 48 square centimeters.
The area of the rectangle is 216 square centimeters.
The area of the irregular figure is 264 square centimeters.
Explanation:
The height of the triangle is the total height of the figure minus the height of the rectangle, that is:
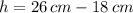
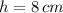
The height of the triangle is 8 centimeters.
The area of the triangle (
 ), measured in square centimeters, is determined by the following formula:
), measured in square centimeters, is determined by the following formula:
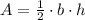 (1)
(1)
Where:
 - Base of the triangle, measured in centimeters.
- Base of the triangle, measured in centimeters.
 - Height of the triangle, measured in centimeters.
- Height of the triangle, measured in centimeters.
If we know that
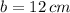 and
and
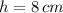 , then the area of the triangle is:
, then the area of the triangle is:
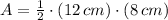

The area of the rectangle is 48 square centimeters.
The area of the rectangle (
 ), measured in square centimeters, is determined by the following formula:
), measured in square centimeters, is determined by the following formula:
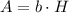 (2)
(2)
Where
 is the height of the rectangle, measured in centimeters.
is the height of the rectangle, measured in centimeters.
If we know that
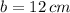 and
and
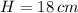 , then the area of the rectangle is:
, then the area of the rectangle is:
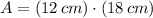
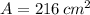
The area of the rectangle is 216 square centimeters.
The area of the irregular figure is the sum of the areas of the rectangle and the triangle. Then, the area of the irregular figure is 264 square centimeters.