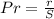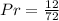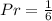Question

Let be the set of permutations of whose first term is a prime. If we choose a permutation at random from , what is the probability that the third term is equal to

Answer 1

`Pr = (1)/(6)`

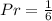
Explanation:

Given

`S = \{1,2,3,4,5\}`

`n = 5`

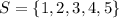
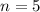
Required

Probability the third term is 3

First, we calculate the possible set.

The first must be prime (i.e. 2, 3 and 5) --- 3 numbers

`2nd \to 4\ numbers`

`3rd \to 3\ numbers`

`4th \to 2\ numbers`

`5th \to 1\ number`

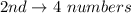
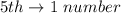
So, the number of set is:

`S = 3 * 4 * 3 * 2 * 1`

`S = 72`

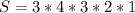
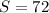
Next, the number of sets if the third term must be 2

`1st \to 2` i.e. 1 or 5

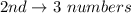`2nd \to 3\ numbers` ---- i.e. remove the already selected first term and the 3rd the compulsory third term

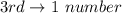`3rd \to 1\ number` i.e. the digit 2

`4th \to 2\ numbers`

`5th \to 1\ number`

So

`r = 2 * 3 * 1 * 2 * 1`

`r = 12`

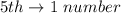
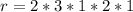
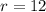
So, the probability is:

`Pr = (r)/(S)`

`Pr = (12)/(72)`

`Pr = (1)/(6)`