Question

Find the TWO integers whos product is -12 and whose sum is 1
​

Answer 1

`\rm Numbers = 4 \ and \ -3.`

Explanation:

Given :-

The sum of two numbers is 1 .

The product of the nos . is 12 .

And we need to find out the numbers. So let us take ,

First number be x

Second number be 1-x .

According to first condition :-

`\rm\implies 1st \ number * 2nd \ number= -12\\\\\rm\implies x(1-x)=-12\\\\\rm\implies x - x^2=-12\\\\\rm\implies x^2-x-12=0\\\\\rm\implies x^2-4x+3x-12=0\\\\\rm\implies x(x-4)+3(x-4)=0\\\\\rm\implies (x-4)(x+3)=0\\\\\rm\implies\boxed{\red{\rm x = 4 , -3 }}`

Hence the numbers are 4 and -3

Answer 2

Explanation:

If the product of 2 integers is -12, then that equation looks like this:

xy = -12

If the sum of those same 2 integers in 1, then that equation looks like this:

x + y = 1

Let's solve the second equation for x and plug it into the first equation. Solving the second equation for x gives us

x = 1 - y and plug that into the first equation in place of x to get:

(1 - y)y = -12 and

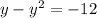`y-y^2=-12` Now move everything over to one side and factor to find y:

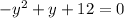`-y^2+y+12=0` and the 2 values for y are

y = -3 and y = 4. Let's see what happens when we solve for x.

If xy = -12 and y is -3:

x(-3) = -12 so

x = 4

If xy = -12 and y is4:

x(4) = -12 so

x = -3

So it looks like the 2 integers are -3 and 4