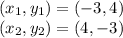Question

Find the TWO integers whos product is -12 and whose sum is 1
​

Answer 1

`\rm Numbers = 4 \ and \ -3.`

Explanation:

Given :-

The sum of two numbers is 1 .

The product of the nos . is 12 .

And we need to find out the numbers. So let us take ,

First number be x

Second number be 1-x .

According to first condition :-

`\rm\implies 1st \ number * 2nd \ number= -12\\\\\rm\implies x(1-x)=-12\\\\\rm\implies x - x^2=-12\\\\\rm\implies x^2-x-12=0\\\\\rm\implies x^2-4x+3x-12=0\\\\\rm\implies x(x-4)+3(x-4)=0\\\\\rm\implies (x-4)(x+3)=0\\\\\rm\implies\boxed{\red{\rm x = 4 , -3 }}`

Hence the numbers are 4 and -3

Answer 2

`\displaystyle( {x}_(1) , y_(1)) =( - 3,4)\\ (x _(2), y_(2)) = (4, - 3)`

Explanation:

we are given two conditions

1. two integers whos product is -12
2. two integers whos sum is 1

let the two integers be x and y respectively according to the first condition

`\displaystyle xy = - 12`

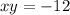
according to the second condition:

`\displaystyle x + y = 1`

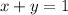
now notice that we have two variables therefore ended up with a simultaneous equation so to solve the simultaneous equation cancel x from both sides of the second equation which yields:

`\displaystyle y = 1 - x`

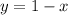
now substitute the got value of y to the first equation which yields:

`\displaystyle x(1 - x) = - 12`

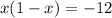
distribute:

`\displaystyle x- {x}^(2) = - 12`

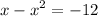
add 12 in both sides:

`\displaystyle x- {x}^(2) + 12 = 0`

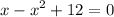
rearrange it to standard form:

`\displaystyle - {x}^(2) + x + 12 = 0`

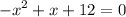
divide both sides by -1:

`\displaystyle {x}^(2) - x - 12 = 0`

factor:

`\displaystyle ({x} + 3)(x - 4) = 0`

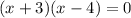
by Zero product property we acquire:

`\displaystyle {x} + 3 = 0\\ x - 4= 0`

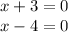
solve the equations for x therefore,

`\displaystyle {x}_(1) = - 3\\ x _(2) = 4`

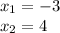
when x is -3 then y is

`\displaystyle y _(1)= 1 - ( - 3)`

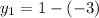
simplify

`\displaystyle y _(1)= 4`

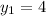
when x is 4 y is

`\displaystyle y _(2)= 1 - ( 4)`

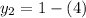
simplify:

`\displaystyle y _(2)= - 3`

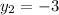
hence,

`\displaystyle( {x}_(1) , y_(1)) =( - 3,4)\\ (x _(2), y_(2)) = (4, - 3)`