Question

Find the TWO integers whos product is -12 and whose sum is 1
​

Answer 1

`\rm Numbers = 4 \ and \ -3.`

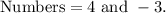
Explanation:

Given :-

The sum of two numbers is 1 .

The product of the nos . is 12 .

And we need to find out the numbers. So let us take ,

First number be x

Second number be 1-x .

According to first condition :-

`\rm\implies 1st \ number * 2nd \ number= -12\\\\\rm\implies x(1-x)=-12\\\\\rm\implies x - x^2=-12\\\\\rm\implies x^2-x-12=0\\\\\rm\implies x^2-4x+3x-12=0\\\\\rm\implies x(x-4)+3(x-4)=0\\\\\rm\implies (x-4)(x+3)=0\\\\\rm\implies\boxed{\red{\rm x = 4 , -3 }}`

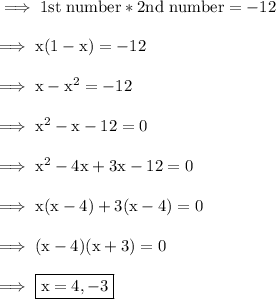
Hence the numbers are 4 and -3

Answer 2

Explanation:

`numbers \: = x \: and \: y \\ x * y = - 12......(1) \\ x + y = 1..... ..(2) \\y = 1 - x \\ put \: this \: in \: (1) \\ x(1 - x) = - 12 \\ x - {x}^(2) = - 12 \\ - x + {x}^(2) - 12 = 0 \\ factorise \\ {x}^(2) - 4x + 3x - 12 = 0 \\ x(x - 4) + 3(x - 4) = 0 \\ (x - 4)(x + 3) = 0 \\ x = + 4 \: or \: - 3 \\ thank \: you`