Question

Find the TWO integers whos product is -12 and whose sum is 1
​

Answer 1

Let integers be x and x-1

ATQ

• x+x-1=1

`\\ \sf\longmapsto 2x-1=1`

`\\ \sf\longmapsto 2x=1+1`

`\\ \sf\longmapsto 2x+2`

`\\ \sf\longmapsto x=(2)/(2)`

`\\ \sf\longmapsto x=1`

Now

`\\ \sf\longmapsto x-1=1-1=0`

• The integers are 1 and 0

But

Integers can be x and 1-x as their sum is 1

`\\ \sf\longmapsto x(1-x)=-12`

`\\ \sf\longmapsto x- x^2=-12`

`\\ \sf\longmapsto x^2-x-12=0`

`\\ \sf\longmapsto x^2-4x+3x-12=0`

`\\ \sf\longmapsto x(x-4)+3(x-4)=0`

`\\ \sf\longmapsto (x-4)(x+3)=0`

`\\ \sf\longmapsto x=4,-3`

Answer 2

`\rm Numbers = 4 \ and \ -3.`

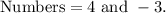
Explanation:

Given :-

The sum of two numbers is 1 .

The product of the nos . is 12 .

And we need to find out the numbers. So let us take ,

First number be x

Second number be 1-x .

According to first condition :-

`\rm\implies 1st \ number * 2nd \ number= -12\\\\\rm\implies x(1-x)=-12\\\\\rm\implies x - x^2=-12\\\\\rm\implies x^2-x-12=0\\\\\rm\implies x^2-4x+3x-12=0\\\\\rm\implies x(x-4)+3(x-4)=0\\\\\rm\implies (x-4)(x+3)=0\\\\\rm\implies\boxed{\red{\rm x = 4 , -3 }}`

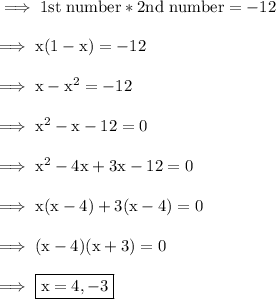
Hence the numbers are 4 and -3