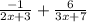Question

The partial fraction decomposition of 9 x 11 6 x 2 23 x 21 can be written in the form of f ( x ) 2 x 3 g ( x ) 3 x 7 , where

Answer 1

`f(x) = -1`

`g(x) =6`

`(-1)/(2x + 3) + (6)/(3x + 7)`

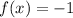
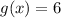
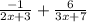
Explanation:

The question is unreadable, however the real polynomial is:

The polynomial fraction is:

`P = (9x + 11)/(6x^2 + 23x + 21)`

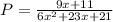
And the decomposition is:

`(f(x))/(2x + 3) + (g(x))/(3x + 7)`

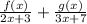
The solution is as follows:

`P = (f(x))/(2x + 3) + (g(x))/(3x + 7)`

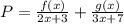
Substitute the expression for P

`(9x + 11)/(6x^2 + 23x + 21) = (f(x))/(2x + 3) + (g(x))/(3x + 7)`

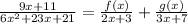
Expand the numerator of the polynomial

`(9x + 11)/((2x + 3)(3x + 7)) = (f(x))/(2x + 3) + (g(x))/(3x + 7)`

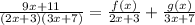
Take LCM

`(9x + 11)/((2x + 3)(3x + 7)) = (f(x)*(3x + 7) + g(x)*(2x + 3))/((2x + 3)(x + 7))`

Cancel out both denominators

`9x + 11} = f(x)*(3x + 7) + g(x)*(2x + 3)`

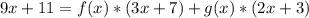
Represent f(x) as A and g(x) as B

`9x + 11} = A*(3x + 7) + B*(2x + 3)`

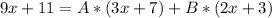
Open bracket

`9x + 11} = 3Ax + 7A + 2Bx + 3B`

`9x + 11} = 3Ax + 2Bx+ 7A + 3B`

`9x + 11} = (3A + 2B)x+ 7A + 3B`

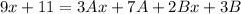
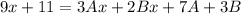
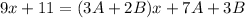
By comparison:

`3A + 2B = 9` ---- (1)

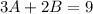`7A + 3B =11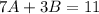` ---- (2)

Make B the subject in (1)

`B = (9 - 3A)/(2)`

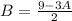
Substitute
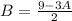`B = (9 - 3A)/(2)` in (2)

`7A + 3((9 - 3A)/(2)) = 11`

Multiply through by 2

`2*7A +2* 3((9 - 3A)/(2)) = 11*2`

`14A + 3(9 - 3A) = 22`

`14A + 27 - 9A = 22`

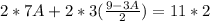
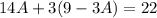
Collect Like Terms

`14A - 9A = 22-27`

`5A = -5`

`A = (-5)/(5)`

`A = -1`

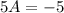
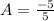
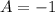
Recall that:

`B = (9 - 3A)/(2)`

`B = (9 - 3 * -1)/(2)`

`B = (9 + 3)/(2)`

`B = (12)/(2)`

`B = 6`

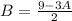
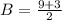
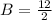
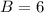
A = -1 and B = 6

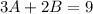`3A + 2B = 9` ---- (1)

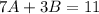`7A + 3B =11` ---- (2)

So:

`f(x) = A`

`f(x) = -1`

`g(x) =B`

`g(x) =6`

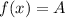
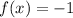
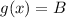
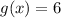
And the decomposition is:

`(-1)/(2x + 3) + (6)/(3x + 7)`