Answer:
(a)
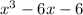
(b) Proved
Explanation:
Given
![r = $\sqrt[3]{2} + \sqrt[3]{4}$](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/66x6zebplduhyoe2d3ti7c.png) --- the root
--- the root
Solving (a): The polynomial
A cubic function is represented as:

Expand
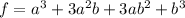
Rewrite as:
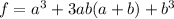
The root is represented as:

By comparison:
![a = $\sqrt[3]{2}](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/g2l04zqdbrz7ciqduotz17.png)
![b = \sqrt[3]{4}$](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/vqp6avlu2al1iggqstqf7g.png)
So, we have:
![f = ($\sqrt[3]{2})^3 + 3*$\sqrt[3]{2}*\sqrt[3]{4}$*($\sqrt[3]{2} + \sqrt[3]{4}$) + (\sqrt[3]{4}$)^3](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/gryt5qkdprqd5x0m6ffju8.png)
Expand
![f = 2 + 3*$\sqrt[3]{2*4}*($\sqrt[3]{2} + \sqrt[3]{4}$) + 4](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/dtl6opw2btckcoy98de7rp.png)
![f = 2 + 3*$\sqrt[3]{8}*($\sqrt[3]{2} + \sqrt[3]{4}$) + 4](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/itrq89w6lnq8v8n6nt290c.png)
![f = 2 + 3*2*($\sqrt[3]{2} + \sqrt[3]{4}$) + 4](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/4wj2bi6i3v0m4pfj9xagld.png)
![f = 2 + 6($\sqrt[3]{2} + \sqrt[3]{4}$) + 4](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/jq4yfmu6sr6n23s0qrtubp.png)
Evaluate like terms
![f = 6 + 6($\sqrt[3]{2} + \sqrt[3]{4}$)](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/igryvwgub1jcjn5v7grtya.png)
Recall that:
![r = $\sqrt[3]{2} + \sqrt[3]{4}$](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/66x6zebplduhyoe2d3ti7c.png)
So, we have:

Equate to 0
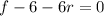
Rewrite as:
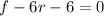
Express as a cubic function
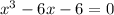
Hence, the cubic polynomial is:
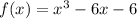
Solving (b): Prove that r is irrational
The constant term of
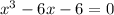 is -6
is -6
The divisors of -6 are: -6,-3,-2,-1,1,2,3,6
Calculate f(x) for each of the above values to calculate the remainder when f(x) is divided by any of the above values
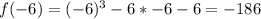
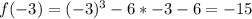
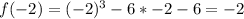
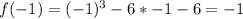
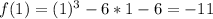
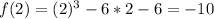
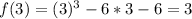
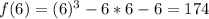
For r to be rational;
The divisors of -6 must divide f(x) without remainder
i.e. Any of the above values must equal 0
Since none equals 0, then r is irrational