Answer:
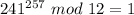
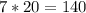
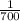
Explanation:
Solving (a): 241^257 mod 12
To do this, we simply calculate
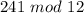
Because
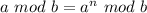
The highest number less than or equal to 241 that is divisible by 12 is 240; So:
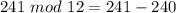
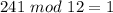
Hence:
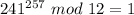
Solving (b): 7 * 20
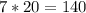
Solving (c): Multiplicative inverse of 7 in 719
The position of 7 in 719 is 700
So, the required inverse is 1/700 ---- i.e. we simply divide 1 by the number