Answer:
Yes, it is possible to have a relation on the set {a, b, c} that is both symmetric and transitive but not reflexive
Explanation:
Let
Set A={a,b,c}
Now, define a relation R on set A is given by
R={(a,a),(a,b),(b,a),(b,b)}
For reflexive
A relation is called reflexive if (a,a)
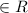 for every element a
for every element a
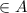
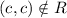
Therefore, the relation R is not reflexive.
For symmetric
If
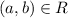 then
then
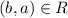
We have
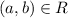 and
and
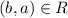
Hence, R is symmetric.
For transitive
If (a,b)
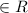 and (b,c)
and (b,c)
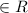 then (a,c)
then (a,c)
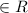
Here,
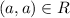 and
and
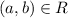
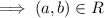
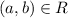 and
and
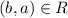
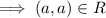
Therefore, R is transitive.
Yes, it is possible to have a relation on the set {a, b, c} that is both symmetric and transitive but not reflexive.