Question

In a liquid with a density of 1500 kg/m3, longitudinal waves with a frequency of 410 Hz are found to have a wavelength of 7.80 m. Calculate the bulk modulus of the liquid.

Answer 1

The bulk modulus of the liquid is 1.534 x 10¹⁰ N/m²

Step-by-step explanation:

Given;

density of the liquid, ρ = 1500 kg/m³

frequency of the wave, F = 410 Hz

wavelength of the sound, λ = 7.80 m

The speed of the wave is calculated as;

v = Fλ

v = 410 x 7.8

v = 3,198 m/s

The bulk modulus of the liquid is calculated as;

`V = \sqrt{(B)/(\rho) } \\\\V^2 = (B)/(\rho)\\\\B = V^2 \rho\\\\B = (3,198 \ m/s)^2 * 1500 \ kg/m^3\\\\B = 1.534 \ * 10^(10) \ N/m^2`

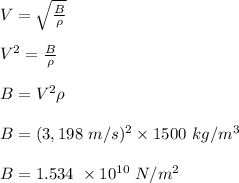
Therefore, the bulk modulus of the liquid is 1.534 x 10¹⁰ N/m²