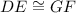Question

In the diagram, DG ∥ EF.

On a coordinate plane, quadrilateral D E F G is shown. Point D is at (negative 2, 2), point G is at (1, 2), point F is at (3, negative 3), and point E is at (negative 4, negative 3).

What additional information would prove that DEFG is an isosceles trapezoid?

DE ≅ GF
DE ≅ DG
EF ≅ DG
EF ≅ GF

Answer 1

Answer:DE ≅ GF

Explanation:

cause i said so

Answer 2

`DE \cong GF`

Explanation:

Given

See attachment for quadrilateral

Required

What proves DEFG as isosceles trapezoid

The non-parallel sides of an isosceles trapezoid are similar and equal.

From the attached quadrilateral, the non-parallel sides are: DE and GF

Hence, for DEFG to be an isosceles trapezoid;

`DE \cong GF`