Answer:
The ratio of f at the higher temperature to f at the lower temperature is 5.356
Step-by-step explanation:
Given;
activation energy, Ea = 185 kJ/mol = 185,000 J/mol
final temperature, T₂ = 525 K
initial temperature, T₁ = 505 k
Apply Arrhenius equation;
![Log((f_2)/(f_1) ) = (E_a)/(2.303 * R) [(1)/(T_1) -(1)/(T_2) ]](https://img.qammunity.org/2022/formulas/chemistry/college/eck06u46jmmmdhmafrhkxtpv2w1zaecxn6.png)
Where;
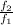 is the ratio of f at the higher temperature to f at the lower temperature
is the ratio of f at the higher temperature to f at the lower temperature
R is gas constant = 8.314 J/mole.K
![Log((f_2)/(f_1) ) = (E_a)/(2.303 * R) [(1)/(T_1) -(1)/(T_2) ]\\\\Log((f_2)/(f_1) ) = (185,000)/(2.303 * 8.314) [(1)/(505) -(1)/(525) ]\\\\Log((f_2)/(f_1) ) = 0.7289\\\\(f_2)/(f_1) = 10^(0.7289)\\\\(f_2)/(f_1) = 5.356](https://img.qammunity.org/2022/formulas/chemistry/college/w6ntakmv7lfvyy936rv67xzkyv65nvdhce.png)
Therefore, the ratio of f at the higher temperature to f at the lower temperature is 5.356