Answer: (1,4)
======================================================
Step-by-step explanation:
The notation <-5,2> is the same as writing the translation rule
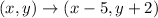
It says: move 5 units to the left and 2 units up
The point (6,2) moves to (1,2) when moving five units to the left. Then it ultimately arrives at (1, 4) after moving 2 units up. You could move 2 units up first and then 5 units to the left later on, and you'd still arrive at (1, 4). In this case, the order doesn't matter (some combinations of transformations this won't be the case and order will matter).
---------
Or you could write out the steps like so
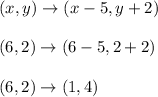
We see that (6,2) moves to (1, 4)