Question

What is the equation of the line that passes through the points (-3,-9) and (5,23)​

Answer 1

Hi there! Your answer is y = 4x+3

Please see the explanation for a clear understanding to the problem.

Any questions about the answer/explanation, feel free to ask in comment! :)

Explanation:

Goal

• Find the equation of a line.

Given

• Two coordinate points which are (-3,-9) and (5,23)

Step 1

• Find the slope by using the formula/rise over run.

You can either plot these points and use your graph-looking method to find a slope without any calculations! (It's possible!). But I'll demonstrate the usage of rate of changes instead of graph method.

Here's a formula that you will need to find a slope.

`m=\HUGE{(y_2-y_1)/(x_2-x_1)}`

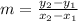
We simply substitute the coordinate points in the formula. Remember the coordinate carefully as It's (x,y) and not (y,x).

`m=(23-(-9))/(5-(-3)) \\m=(23+9)/(5+3)\\m=(32)/(8) \\m=4`

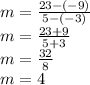
Therefore, our slope is 4. But since we want to find the entire equation as well, we can't just answer only a slope. Therefore, let's proceed to the next step.

Step 2

• Rewrite the equation in slope-intercept form.

Let's see the form of slope-intercept. Make sure to remember carefully as you might be confused with point-slope form.

`\large{y=mx+b} \Longrightarrow \large\sf{slope-intercept \ form}\\`

`\large{y=m(x-x_1)+y_1} \Longrightarrow \large\sf{point-intercept \ form}`

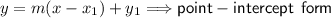
The equation of a line is mostly in slope-intercept form so we will do slope-intercept form instead.

From the step 1, we solved and got the value of slope which is m from y = mx+b. We substitute m = 4 in the slope-intercept form.

`y=mx+b\\y=4x+b`

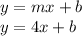
Notice that b-term is still missing! We need to find the b-term for the equation to be completed. Proceed to the next step.

Step 3

• Find the value of b.

From the y = mx+b where m = slope and b = y-intercept. Finding the value of b can be different, depending on the equation itself. For this scenario, we have to substitute any given coordinate points in the equation. Remember (x,y) coordinate as well. You can either choose to substitute only one coordinate point if you are pretty certain but substituting two coordinate points in an equation is highly advised for a beginner.

Step 3.1

• Substitute (-3,-9) in the equation.

`y=4x+b`

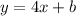
Substitute x = -3 and y = -9 in the equation.

`-9=4(-3)+b\\-9=-12+b\\-9+12=b\\3=b`

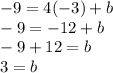
Step 3.2

• Substitute x = 5 and y = 23 in the equation.

`y=4x+b\\23=4(5)+b\\23=20+b\\23-20=b\\3=b`

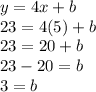
Since both equations have b = 3 as the solution. We can conclude that b = 3 is the solution to y = mx+b.

Step 4

• Rewrite the equation again by substituting b = 3 in.

From y = 4x+b

`y=4x+b\\`

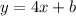
Substitute b = 3 in the equation as we get:
`y=4x+3` #