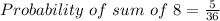Answer:
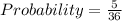
Explanation:
The samples are
{ ( 1 , 1) , ( 1 , 2 ) , ( 1 , 3 ) , ( 1 , 4 ) , ( 1 , 5) , ( 1 , 6 )
( 2 , 1 ) , ( 2 2 ) , ( 2 , 3 ) , ( 2 , 4 ) , ( 2 , 5 ) , ( 2 , 6 )
( 3 , 1 ) , ( 3 , 2 ) , ( 3 , 3 ) , ( 3 , 4 ) , ( 3 , 5 ) , ( 3 , 6 )
( 4 , 1 ) , ( 4 , 2 ) , ( 4 , 3 ) , ( 4 , 4 ) , ( 4 , 5 ) , ( 4 , 6 )
( 5 , 1 ) , ( 5 , 2 ) , ( 5 , 3 ) , ( 5 , 4 ) , ( 5 , 5 ) , ( 5 , 6 )
( 6 , 1 ) , ( 6 , 2 ) , ( 6 , 3 ) , ( 6 , 4 ) , ( 6 , 5 ) , ( 6 , 6 ) }
Total number of samples = 36
Samples with a sum of 8 = { ( 2 , 6 ) , ( 3 , 5 ) , ( 4 , 4 ) , ( 5 , 3 ) , ( 6 , 2 ) }
Total number of sample with sum 8 = 5
Therefore,