Question

g Galileo's telescopes were not of high quality by modern standards. He was able to see the moons of Jupiter, but he never reported seeing features on Mars. Use the small-angle formula to find the angular diameter of Mars when it is closest to Earth. How does that compare with the maximum angular diameter of Jupiter

Answer 1

θ₂/ θ₁= 2.58

Step-by-step explanation:

In this exercise you are asked to compare the angular diameters of Mars and Jupiter. The angular diameter or angle in radians is

θ = D / R

where D is the diameter of the body, the distance from Earth to the body of interest and θ is angle in radians

The different distances are tabulated with respect to the Sun

Sun -Earth 1,496 10¹¹ m

Sun- Mars 2.28 10¹¹ m

Sun - Jupiter 7.78 10 m

The Radii of the planets are

Mars 3.37 10⁶ m

Jupiter 6.99 10⁷ m

let's calculate the angles for each body

a) Mars

θ₁ = 2r / R'

the distance from the ground is

R ’= D_planet - D_earth

R ’= 2.28 10¹¹ - 1.496 10¹¹

R ’= 0.784 10¹¹ m

let's calculate

θ₁ =
`(2 \ 3.37 \ 10^6 )/(0.784 \ 10^(11))`

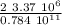
θ₁ = 8.6 10⁻⁵ radians

b) Jupiter

R ’= 7.78 10¹¹ - 1.496 10¹¹

R ’= 6.284 10¹¹ m

let's calculate

θ₂ =
`(2 \ 6.99 \ 10^7)/(6.284 \ 10^(11))`

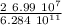
θ₂ = 2.22 10⁻⁴ radians

the ratio of the angular diameters is

θ₂/ θ₁ =
`(2.22 \ 10^(-4))/(8.6 \ 10^(-5))`

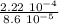
θ₂/ θ₁= 2.58