Answer:
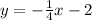
Explanation:
i'm not sure if you're trying to find the equation of the line ?? but i'll assume that's the case and find the slope-intercept form equation of the line.
slope intercept form is
 , where
, where
 is the slope and
is the slope and
 is the y-intercept. since the slope is already identified, you can plug in
is the y-intercept. since the slope is already identified, you can plug in
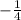 for
for
 .
.
 ⇒
⇒
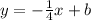
plug in the
 and
and
 values from the coordinate pair that passes through the line, which is (-4, -1). you can start with either
values from the coordinate pair that passes through the line, which is (-4, -1). you can start with either
 or
or
 , but i'm going to start with
, but i'm going to start with
 .
.
first, plug in
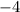 for
for
 .
.
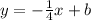 ⇒
⇒
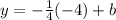
now plug in
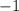 for
for
 .
.
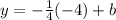 ⇒
⇒
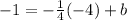
after plugging in all of the given values, the equation is now
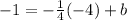 , in which you need to solve for
, in which you need to solve for
 .
.
now it's time to solve! begin by multiplying
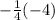 in order to simplify the right side of the equation.
in order to simplify the right side of the equation.
you now have
 . subtract 1 from both sides of the equation. on the right side, it cancels itself out, leaving you with
. subtract 1 from both sides of the equation. on the right side, it cancels itself out, leaving you with
 . on the left side of the equation, you now have
. on the left side of the equation, you now have
 , which equals
, which equals
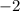 .
.
therefore
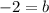 , or
, or
 .
.
now that you've solved for your
 value, plug it into your initial slope-intercept form equation!
value, plug it into your initial slope-intercept form equation!
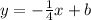 ⇒
⇒
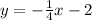
if you want to check to make sure that the values are correct, plug (-4, -1) into your completed slope-intercept form equation. as you did in the beginning, plug in
 for
for
 and
and
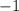 for
for
 .
.
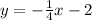 ⇒
⇒
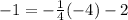
begin simplifying by multiplying
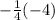 .
.
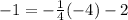 ⇒
⇒

subtract
 .
.
 ⇒
⇒
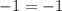
since both sides of the equation are equal, that means your
 value of
value of
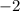 is correct because it makes the equation true!
is correct because it makes the equation true!
aaaand there you go! i hope this helps. have a great day! <3