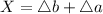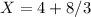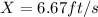Answer:
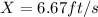
Explanation:
From the question we are told that:
Height of pole
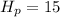
Height of man
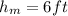
Speed of Man
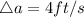
Distance from pole
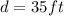
Let
Distance from pole to man=a
Distance from man to shadow =b
Therefore

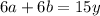
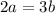
Generally the equation for change in velocity is mathematically given by

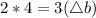
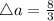
Since
The speed of the shadow is given as