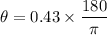Question

Starting from rest, a Ferris wheel of diameter 30.0 m undergoes an angular acceleration of 0.0400 rad/s2. A certain rider is at the lowest point of the wheel just as it starts to move.

A) Find the velocity of the rider just as he completes a quarter of a turn.
B) Find the radial and tangential components of his acceleration at the same point.
C) How much farther must the wheel turn before the rider attains a speed of 6.00 m/s (the maximum that occurs during the ride)?
a. 5.32 m/s, up.
b. 0.600 m/s2, up.
1.88 m/s2 toward center.
d. 24.6°.

Answer 1

Given :

Diameter, D = 30 m

∴ Radius, R = 15 m

Angular acceleration, α = 0.044
`$rad/s^2$`

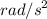
a). Velocity of the rider just as he completes a quarter of a turn is :

`$\omega_i = 0 \ rad/s$`

`$\theta = (\pi)/(2)\ rad$`

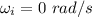
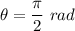
V = R ω

∴
`$\omega^2_f=\omega^2_i + 2 \alpha \theta$`

`$\omega^2_f=0+ 2 * 0.04 * (\pi)/(2)$`

`$\omega^2_f=0.1256$`

`$\omega = √(0.1256)$`

`$=0.354 \ rad/s$`

∴
`$V=R \omega_f$`

`$= 15 * 0.354$`

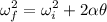
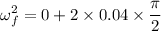
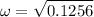
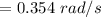
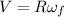
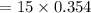
= 5.32 m/s up

b). Tangential acceleration

`$a_T= \alpha R$`

= 0.04 x 15

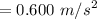`$= 0.600 \ m/s^2$` up

Radial acceleration,

`$a_r=(V^2)/(R)$`

`$=((5.32)^2)/(15)$`

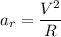
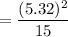
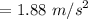`$= 1.88 \ m/s^2$` towards center.

c). Final angular velocity

given :
`$V_0 = 6 \ m/s$`

`$\omega_i = 0.354 \ rad/s$`

`$\alpha = 0.0400 \ rad/s^2$`

`$\omega_f = (6)/(15) \ rad/s$`

`$\omega^2_f=\omega^2_i + 2 \alpha \theta$`

`$\left((6)/(15)\right)^2=(0.354)^2 + 2 * 0.04 * \theta$`

`$\theta = (0.16-0.1256)/(2 * 0.04)$`

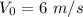
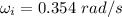
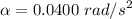
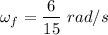
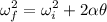
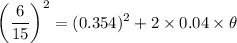
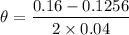
= 0.43 rad

or
`$\theta = 0.43 * (180)/(\pi)$`

`$24.6^\circ$`