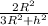Answer:
h1/h2 =
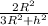
Step-by-step explanation:
Using two rolls of tissue paper : One roll dropped normally while the other drops as some holds onto a sheet of the toilet paper ( I.e. the tissue paper drops rotating about its axis )
Determine the ratio of heights h1/h2
mass of tissues = same
radius of tissues = same
h1 = height of tissue 1
h2 = height of tissue 2
For the first tissue ( Tissue that dropped manually )
potential energy = kinetic energy
mgh = 1/2 mv^2
therefore the final velocity ( v^2 ) = 2gH ----- ( 1 )
second tissue ( Tissue that dropped while rotating )
gh =
 ( 3 +
( 3 +
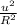 ) ------ ( 2 )
) ------ ( 2 )
To determine the ratio of heights we will equate equations 1 and 2
hence :
gh =
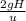 ( 3 +
( 3 +
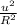 )
)
∴ h1/h2 =