Question

10

What are the x- and y-coordinates of point E, which
partitions the directed line segment from A to B into a
ratio of 1:2?
B(-4,9)
9
8
X E
(
mn)(x2 – xı) + x
7-
6
5
4
mm. )(x2 - y) + y
3
-7 -6 -5 4 -3 -2 -14
2 3 4 5 6 7
0 (0, 1)
0 (-1,3)
O(-2,5)
(1,0)
X
-2.
3
A(2,-3)
19

Answer 1

Explanation:

The formulas to find the x and y coordinates of E are:

`x=(bx_1+ax_2)/(a+b)` and
`y=(by_1+ay_2)/(a+b)` where x1, x2, y1, and y2 are from the coordinates of A and B, and a = 1 (from the ratio) and b = 2 (from the ratio). Filling in to find x first:

`x=(2(2)+1(-4))/(1+2)=(4-4)/(3)=0` and now for y:

`y=(2(-3)+1(9))/(1+2)=(-6+9)/(3)=(3)/(3)=1`

The coordinates of E are (0, 1).

Answer 2

Given:

The points are A(2,-3) and B(-4,9).

The point E divides the segment AB in 1:2.

To find:

The coordinates of point E.

Solution:

Section formula: If a point divides a line segment in m:n, then the coordinates of the point is:

`Point=\left((mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n)\right)`

Using the section formula, the coordinates of point E are:

`E=\left((1(-4)+2(2))/(1+2),(1(9)+2(-3))/(1+2)\right)`

`E=\left((-4+4))/(3),(9-6)/(3)\right)`

`E=\left((0))/(3),(3)/(3)\right)`

`E=\left(0,1\right)`

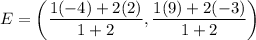
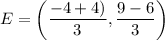
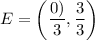
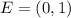
Therefore, the coordinates of the point E are (0,1).