Answer and Step-by-step explanation: This function is a probability density function of a random variable X:

and to calculate probabilities, we will have to integrate it:
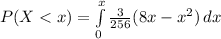
Solving:
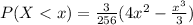
Then:
a. P(X < 5)
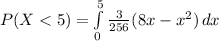
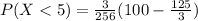
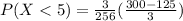
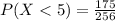
P(X < 5) = 0.683
b. P(X < 9)
Since density function's upper limit is 8, probability of x < 9 is 100% or 1.
So, P(X < 9) = 1
c. P(5 < X < 7)
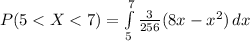
![P(5<X<7)=(3)/(256)[4(7)^(2)-(7^(3))/(3)-4(5)^(2)+(5^(3))/(3)]](https://img.qammunity.org/2022/formulas/mathematics/college/dbk9llbf98v9qz84u51mr5dkhmay4n2mxu.png)
![P(5<X<7)=(3)/(256)[96-(218)/(3) ]](https://img.qammunity.org/2022/formulas/mathematics/college/tcc0l0pijvu66jy27k4wck0sz1rxqnzbe0.png)
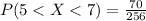
P(5 < X < 7) = 0.273
d. P(X > 3)
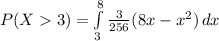
![P(X>3)=(3)/(256)[256-(512)/(3)-36+9 ]](https://img.qammunity.org/2022/formulas/mathematics/college/ea5hkvycpfzkhnjqvod2te1ja7bselawfc.png)

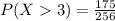
P (X > 3) = 0.683
e. P(X < x) = 0.95
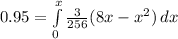
![(3)/(256)[(12x^(2)-x^(3))/(3) ] =0.95](https://img.qammunity.org/2022/formulas/mathematics/college/9pp4lygtyuccbj5ttr0k3sl0gkcvo9wr02.png)
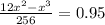

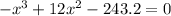
Solving this cubic equation, we have three values for x:
x₁ = -3.909
x₂ = 8.992
x₃ = 6.917
The value of x will the one between 0 and 8, which are the limits of the function. So, value of x which gives a probability of 0.95 is x = 6.917.