Answer:
1. Since
 and
and
 , these conditions are met.
, these conditions are met.
2. Approximately normal.
3. 0.35
4. 0.0389
Explanation:
Central Limit Theorem:
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
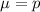 and standard deviation
and standard deviation
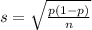 , as long as
, as long as
 and
and

Let's say you want to poll a random sample of 150 students on campus to see if they prefer to take online classes.
This means that
 .
.
35% of all students actually prefer to take classes online
This means that
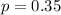
1. Discuss the conditions necessary to use the normal curve to model this sampling distribution and explain whether or not they are met.
The conditions necessary are
 and
and
 .
.
We have that
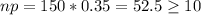
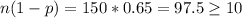
Since
 and
and
 , these conditions are met.
, these conditions are met.
2. If the normal model is appropriate for this distribution, what shape would you expect it to have?
By the Central Limit Theorem, approximately normal.
3. If you were to use the normal model for this p-hat sampling distribution, what value would be at the center of your sampling distribution? In other words, what value would all of those sample proportions center around?
The mean, which by the Central Limit Theorem, is
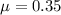 .
.
4. What would be the standard deviation of this sampling distribution?
By the Central Limit Theorem,
