Question

Dual-energy X-ray absorptiometry (DXA) is a technique for measuring bone health. One of the most common measures is total body bone mineral content (TBBMC). A highly skilled operator is required to take

asked Sep 25, 2022 2.6k views

Dual-energy X-ray absorptiometry (DXA) is a technique for measuring bone health. One of the most common measures is total body bone mineral content (TBBMC). A highly skilled operator is required to take the measurements. Recently, a new DXA machine was purchased by a research lab and two operators were trained to take the measurements. TBBMC for eight subjects was measured by both operators. The units are grams (g). A comparison of the means for the two operators provides a check on the training they received and allows us to determine if one of the operators is producing measurements that are consistently higher than the other. Here are the data:

Subject
Operator 1 2 3 4 5 6 7 8
1 1.326 1.337 1.079 1.229 0.936 1.009 1.179 1.289
2 1.323 1.322 1.073 1.233 0.934 1.019 1.184 1.304
Take the difference between the TBBMC recorded for Operator 1 and the TBBMC for Operator 2. (Operator 1 minus Operator 2. Round your answers to four decimal places.)
X-bar=
S=
Describe the distribution of these differences using words. (which one is correct)
A. The distribution is left skewed.
B. The sample is too small to make judgments about skewness or symmetry.
C. The distribution is uniform.
D. The distribution is uniform.
E. The distribution is Normal.

Dominick Pastore asked

by Dominick Pastore

5.2k points

1 Answer

Ask a Question

Diogo Barroso · Answer 1 · 2022-09-30T19:56:18+0000

Answer:

(a)

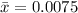
$\bar x = 0.0075$

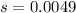
s = 0.0049

(b)

B. The sample is too small to make judgments about skewness or symmetry.

Explanation:

Given:

n = 8

$\begin{array}{ccccccccc}{} & {S} & {u} & {b} &{j} & {e} & {c} & {t} & {s} &{Operator} & {1} & {2} & {3} & {4} & {5} & {6} & {7} & {8} & {1} & 1.326 & 1.337 & 1.079 & 1.229 & 0.936 & 1.009 & 1.179 & 1.289 & 2 & 1.323 & 1.322 & 1.073 & 1.233 & 0.934 & 1.019 & 1.184 & 1.304 \ \end{array}$

Solving (a):

First, calculate the difference between the recorded TBBMC for both operators:

$\begin{array}{ccccccccc}{} & {S} & {u} & {b} &{j} & {e} & {c} & {t} & {s} &{Operator} & {1} & {2} & {3} & {4} & {5} & {6} & {7} & {8} & {1} & 1.326 & 1.337 & 1.079 & 1.229 & 0.936 & 1.009 & 1.179 & 1.289 & 2 & 1.323 & 1.322 & 1.073 & 1.233 & 0.934 & 1.019 & 1.184 & 1.304 & &0.003 & 0.015 & 0.006 & 0.004 & 0.002 & 0.010 & 0.005 & 0.015 \ \end{array}$

The last row which represents the difference between 1 and 2 is calculated using absolute values. So, no negative entry is recorded.

The mean is then calculated as:

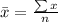
$\bar x = (\sum x)/(n)$

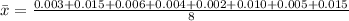
$\bar x = (0.003 + 0.015 + 0.006 + 0.004 + 0.002 + 0.010 + 0.005 + 0.015)/(8)$

$\bar x = (0.06)/(8)$

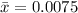
$\bar x = 0.0075$

Next, calculate the standard deviation (s).

This is calculated using:

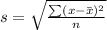
$s = \sqrt{(\sum (x - \bar x)^2)/(n)}$

So, we have

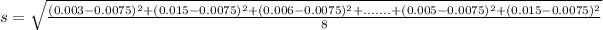
$s = \sqrt((0.003 - 0.0075)^2 + (0.015 - 0.0075)^2+ (0.006- 0.0075)^2+ ....... + (0.005- 0.0075)^2+ (0.015- 0.0075)^2 )/(8)$
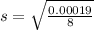
$s = \sqrt(0.00019)/(8)$

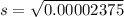
$s = \sqrt{0.00002375$

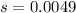
s = 0.0049

Solving (b):

Of the given options (A - E), option B is correct because the sample is actually too small

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions