Question

In the figure below, what is m<1 if m<7= 60 dergrees

Answer 1

○=> Correct option :

`\tt\color{plum}\bold{(A) \: 60}`

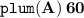
○=> Steps to derive correct option :

Given :

Measure of angle 7 = 60°

Angle 1 and angle 7 are corresponding angles, so their values will be equal.

Which means :

Angle 1 = 60°

Thus, the measure of angle 1 = 60°

Therefore, the correct option is (A) 60