Question

You are working on your family's farm during a summer vacation from school. Your father wants to know how far below ground level the water surface is in a water well. He asks you to determine the depth. He has no suggestions as to how to do this. You look down into the well but cannot see the water surface, so you sit down to think about the challenge. You come up with a solution! You open a frequency generator app on your smartphone, set the volume at its maximum position, and hold the phone over the opening to the well. As you vary the frequency of the sine wave sound emitted by the phone, you notice successive resonances at 54.00 Hz and 59.68 Hz. From these values, you determine the depth of the well. (Enter your answer in m.)

Answer 1

L = 96,4 10³ m

Step-by-step explanation:

After reading this long statement of the problem, we can approximate the well as a tu with one end open and the other end closed, therefore we have two resonance frequencies.

The resonance at the open ends forms a maximum and at the closed ends a node is formed, therefore the standing wave fulfills the relationship

L = λ/ 4 1st harmonic

L = 3 λ/4 3rd harmonic

L = 5 λ/4 5rd harmonic

therefore the general term is

L = n λ/ 4 n = 1, 3, 5, 7 .. (2n + 1)

The speed of sound is related to the donut length and the frequencies

v = λ f

λ = 4L / n

v =
`(4L)/( nf)`

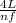
as the speed of sound is a constant

for the initial frequency f = 54 Hz occurs for the number n

340 =
`(4L)/(54 n)`

L / n =
`(340 \ 54)/(4)`

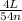
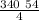
L / n = 4590

for the frequency f = 59.68 Hz it has an odd number n

340 =
`(4L)/(59.68 n')`

L / n '=
`(340 \ 59.68)/(4)`

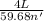
L / n '= 5072.8

we have a system of two unknowns with two equations

L / n = 4590

L / n '= 5072.8

therefore the length is

L = 4590 n = 5072.8 n '

as the two frequencies are very close we can assume that they correspond to consecutive odd numbers

n = 1.1052 n '

n n’ n’ / n

1 3 3

3 5 1.66

5 7 1.4

7 9 1,286

9 11 1.22

11 13 1.18

13 15 1.15

15 17 1.13

17 19 1,117

19 21 1.1052

We can see in the table the two numbers must be n = 19 and n ’= 21

let's calculate the length of the well

L = 4590 21

L = 96390 m

L = 96,4 10³ m