Answer:
(a)
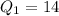
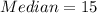
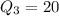
(b)
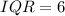
Explanation:
Given
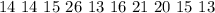

Solving (a): Median and the quartiles
Start by sorting the data
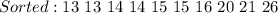
The median position is:
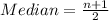
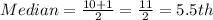
This implies that the median is the average of the 5th and the 6th data;
So;
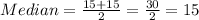
Split the dataset into two halves to get the quartiles
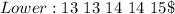
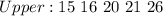
The quartiles are the middle items of each half.
So:
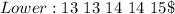
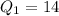 ---- 14 is the middle item
---- 14 is the middle item
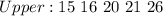
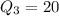 ---- 20 is the middle item
---- 20 is the middle item
Solving (b): The interquartile range (IQR)
This is calculated as:
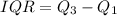
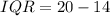
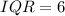
Solving (c): Incomplete details