○=> Correct option :
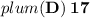
○=> Steps to derive correct answer :
Given :
▪︎Angle (5x)° and angle 95° are supplementary angles.
Which means :
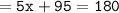
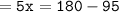
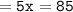

Thus, the value of x = 17
Let us check whether or not we have found out the correct value of x by placing 17 in the place of x:
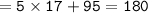
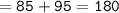
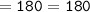
Since the sum of both angles is equivalent to 180[85+95=180], we can conclude that we have found out the correct value of x.
Therefore, the correct option is (D) 17