The correct option is b.
The fourth term in the sequence is
 .
.
To find the fourth term in the arithmetic sequence represented by the recursive formula
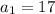 and
and
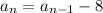 , we can use the recursive formula to generate the terms one by one. Here's a step-by-step process:
, we can use the recursive formula to generate the terms one by one. Here's a step-by-step process:
1. Start with the given value of
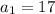 .
.
2. Use the recursive formula to find
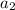 :
:
![\[a_2 = a_1 - 8 = 17 - 8 = 9\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/nr5ouo4kxxfcbp3bnk1qqxh3dlkuze0qb2.png)
3. Use the recursive formula again to find
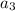 :
:
![\[a_3 = a_2 - 8 = 9 - 8 = 1\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/syxt0s9lgi5ojy3t449hk7pqmfyvn7itoc.png)
4. Finally, use the recursive formula one more time to find
 :
:
![\[a_4 = a_3 - 8 = 1 - 8 = -7\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/qdfzmhtzs0fvd8arl7r4if4xvkjosxfpju.png)
So, the fourth term in the sequence is
 .
.
Therefore, the answer is:
 .
.