Question

PLS HELP ME ASAP PLS ILL MARK BRAIN

Answer 1

665

Explanation:

Answer 2

Explanation:

1). Let the circumference C and area A of the circle are proportional,

C ∝ A

C = kA

Here k = proportionality constant

k =
`(C)/(A)`

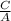
From the given table,

For C = 25 cm, A = 50 cm²

Then the value of k =
`(25)/(50)`

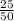
k =
`(1)/(2)`

For C = 50 cm, A = 201 cm²

k =
`(50)/(201)` ≈
`(1)/(4)`

In both the cases proportionality constant is giving the different values.

Therefore, Circumference and Area of the circular objects are not proportional.

2). If A =
`(1)/(2)* r* C`

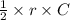
Then this equation will be true for all the values of r and C given in the table.

For r = 4 cm and C = 25 cm

A =
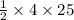`(1)/(2)* 4* 25` = 50 cm²

For r = 8 cm and C = 50 cm

A =
`(1)/(2)* 8* 50`

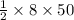
A = 200 cm²

True for all values of 'r' and 'C'.