Answer:

Explanation:
Given that the circle has a radius of 3 feet . And a bigger circle is created so that the ratio of radii of the two circles is 4 : 7 . And we need to find the ratio of the circumferences .
Now we know that the circumference of the circle is given by ,

Now let the circumference of the first circle be
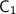 and the circumference of the second circle be
and the circumference of the second circle be
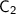 .
.
Finding the ratios :-
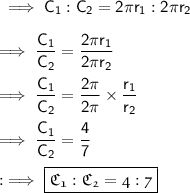
Hence the ratio of the circumferences is same as that of the radius .