Answer:
see explanation
Explanation:
let y = f(x) and rearrange making x the subject, that is
y = 3x - 2 ( add 2 to both sides )
y + 2 = 3x ( divide both sides by 3 )
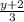 = x
= x
change y back into terms of x with x =
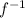 (x)
(x)
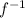 (x) =
(x) =
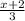
To evaluate
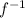 (13) substitute x = 13 into
(13) substitute x = 13 into
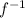 (x) , that is
(x) , that is
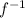 (13) =
(13) =
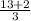 =
=
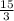 = 5
= 5