Question

A rubber ball is dropped from a height of 10 feet onto a hard surface. After the first bounce, the ball is 6 feet in the air and continues to follow a sequence of bounces. Assume the distances from the ground form a geometric sequence. What is the total DOWNWARD vertical distance the ball has traveled after it hits the surface the 5th time?

Answer 1

The total DOWNWARD vertical distance the ball has traveled after it hits the surface the 5th time is 23.056 feet.

Explanation:

Geometric sequence:

The nth term is a product of the previous(nth-1) term and the common ratio. That is:

`a_n = qa_(n-1)`

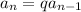
In which q is the common difference.

Sum of the first n terms of geometric sequence:

The sum of the first n terms of a geometric sequence is given by:

`S_n = (a_1(1-q^n))/(1-q)`

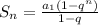
A rubber ball is dropped from a height of 10 feet onto a hard surface.

This means that
`a_1 = 10`

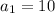
The ball is 6 feet in the air and continues to follow a sequence of bounces

This means that
`q = (6)/(10) = 0.6`

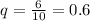
What is the total DOWNWARD vertical distance the ball has traveled after it hits the surface the 5th time?

This is
`S_5`. So

`S_5 = (10(1-0.6^5))/(1-0.6) = 23.056`

The total DOWNWARD vertical distance the ball has traveled after it hits the surface the 5th time is 23.056 feet.